Moore's Law - Is the End Upon Us?

Last Updated: Mon Jan 27 11:18:09 UTC 2014

Moore's Law - Is the End Upon Us?

Originally published July, 2000

by Carlo Kopp

© 2000, 2005 Carlo Kopp

When Gordon Moore of Intel Corp fame formulated Moores Law' during the mid 1960s, he could have neither anticipated the longevity, nor the longer term implications of this simple empirical relationship. Like many of the pervasive observations of twentieth century science, Moore's Law has become, in a rather mangled form, part of the popular culture. This is in a sense unfortunate, since mangled lay interpretations tend to frequently obscure the scientific substance of the matter. Used and abused every which way imaginable, what goes as Moore's Law in the mass media and marketing literature frequently bears little resemblance to the real thing.

In this month's feature we will explore the behaviour of Moore's Law, and also explore what we know at this time about its likely bounds. We will also indulge in some speculation on likely future outcomes. Moore's Law Gordon Moore's empirical relationship is cited in a number of forms, but its essential thesis is that the number of transistors which can be manufactured on a single die will double every 18 months.

The starting point for this exponential growth curve is usually set at 1959 or 1962, the period during which the first silicon planar transistors were designed and tested. Purists will note that Moore defined the rule originally in relation to ICs alone, since the microprocessor was but a twinkle in the eye of a design engineer at that time. 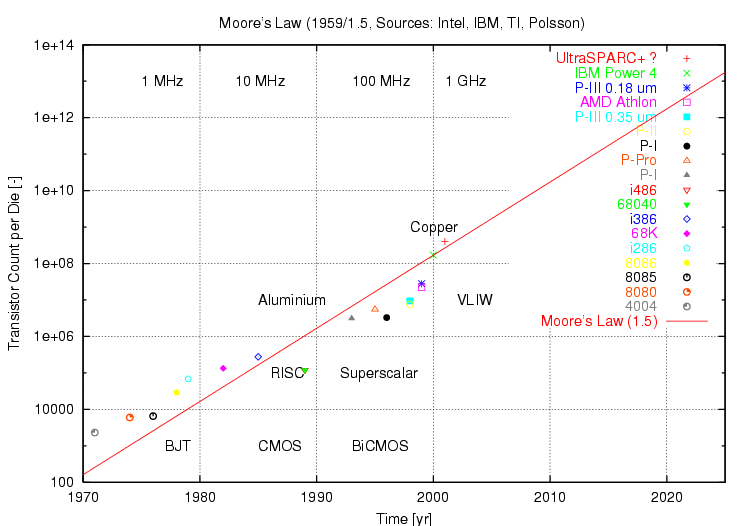We now have four decades of empirical data to validate Moore's argument. Figure 1. depicts a sampling of microprocessor transistor counts, against the basic form of Moore's Law, covering mostly Intel chips but also relevant equivalents.

Clearly the empirical data supports the argument well, even allowing for considerable noise in the data set. The dip during the early nineties is interesting, since it coincides with the early manufacture of superscalar architecture chips. Similar plots for high density Dynamic Random Access Memory (DRAM) devices yield a very similar correlation between Moore's Law and actual device storage capacity. Current projections would indicate 16 Gigabit DRAM devices by 2007.

Two important questions can be raised at this point. The first is that of how do we relate the achievable computing performance of systems to Moores Law'. The second is the critical question of how long will Moores Law hold out'. Both deserve careful examination since both have important implications for our industry. The computing performance of a computer system cannot be easily measured, nor can it be related in a simple manner to the number of transistors in the processor itself.

Indeed, the only widely used measures of performance are various benchmark programs, which serve to provide essentially ordinal comparisons of relative performance for complete systems running a specific benchmark. This is for good reasons, since the speed with which any machine can solve a given problem depends upon the internal architecture of the system, the internal microarchitecture of the processor chip itself, the internal bandwidth of the busses, the speed and size of the main memory, the performance of the disks, the behaviour of the operating system software and the characteristics of the compiler used to generate executable code. The clock speed of the processor chip itself is vital, but in many instances may be less relevant than the aggregated performance effects of other parts of the system.

What can be said is that machines designed with similar internal architectures, using similar operating systems, compilers and running the same compute bound application, will mostly yield benchmark results in the ratios of their respective clock speeds. For instance, a compute bound numerically intensive network simulation I wrote a couple of years ago was run on three different generations of Pentium processor, and a mid 1990s SuperSPARC, all running different variants of Unix, but using the same GCC compiler.

The time taken to compute the simulation scaled, within an error of about 3%, with the inverse ratio of clock frequencies. Indeed, careful study of published benchmarks tends to support this argument. A quick study of the Intel website, www.intel.com, comparing Spec series benchmarks for the Pentium Pro, Pentium II and Pentium III is an excellent example, since all three processors employ variants of the same microarchitecture, but are implemented in progressively faster processes, and span historically a five year period. The caveat in such comparisons is of course that the application is compute bound, and that all systems exhibit similar cache and memory bandwidth.

Large differences in the latter can skew the results of the comparison. The empirical observation that computing performance in like architecture machines scales approximately with the clock frequency of the chip is useful, insofar as it allows us to relate achievable performance to Moore's Law, with some qualifying caveats. Prof Carver Mead of VLSI fame observes that clock speeds scale with the ratio of geometry sizes, as compared to transistor counts which scale with the square of the ratio of geometry sizes.

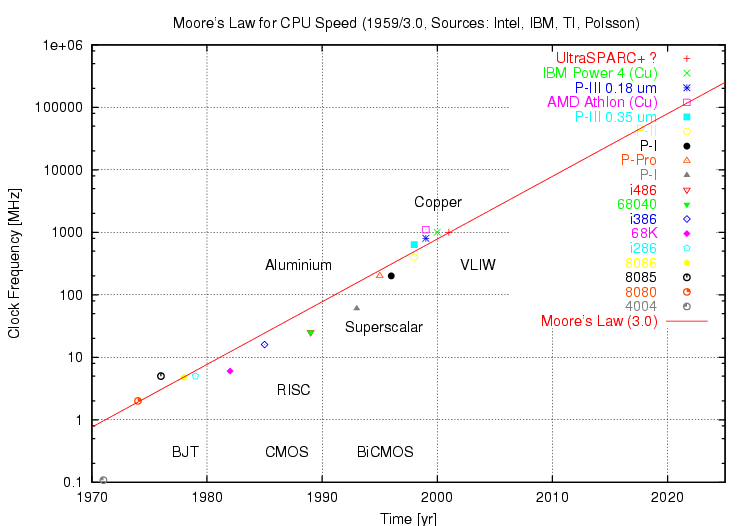
This is important insofar as it defines the relationship between acheivable transistor speed and geometry, as well as imposing a square root relationship between speed and density growth. The interpretation of Moore's Law used in Figure 2. assumes this square root dependency, and incorporates a scaling factor to adjust the frequency to measured data. The plot drawn in Figure 2. thus shows good agreement with Mead's model.

Again we can observe the dip in the empirical data against the process/density curve during the early/mid 1990s. This resulted from reduced commercial pressure for further clock speed gains, in turn resulting from the introduction of superscalar architectures. As all industry players adopted superscalar techniques, pressure to gain performance through process improvements resumed and clock speed curve returned to predicted values. The conclusion that we can draw is that we will see a direct performance gain over time, proportional to the square root of the Moore's Law exponential, in machines with a given class of architecture.

Since most equipment in operational use today is through prior history locked into specific architectures, such as Intel x86, SPARC, PowerPC, Alpha, MIPS and other, the near term consequence is that we will see performance increase exponentially with time for the life of the architecture. However, major changes in internal architecture can produce further gains, at an unchanged clock speed. Therefore, the actual performance growth over time has been greater than that conferred by clock speed gains alone. Higher transistor counts allow for more elaborate internal architectures, thereby coupling performance gains to the exponential growth in transistor counts, in a manner which is not easily scaled like clock speeds.

This effect was observed in microprocessors with the introduction of pipelining in the 1980s, superscalar processing in the 1990s and will be soon observed again with the introduction of VLIW architectures over the next two years. Since we are also about to observe the introduction of copper metallisation during this period, replacing aluminium which has been used since the sixties, we can expect to see a slight excursion above the curve predicted by Moore's Law.

This behaviour relates closely to the second major question, which is that of the anticipated valid life time of Moore's Law. Many predictions have been made over the last two decades in relation to its imminent end, usually accompanied by much commercial or media hype. However, to date every single obstacle in semiconductor fab processes and packaging has been successfully overcome.

Are we being lulled into a state of complacency on this issue, with so many people so frequently crying wolf ? It is not difficult to observe that the limits on the scaling of transistor sizes and thus the achievable transistor counts per die are bounded by quantum physical effects. At some point, carriers will tunnel between structures, rendering transistors unusable and insulators leaky, beyond some point the charge used to define logical states will shrink down to the proverbial single electron.

Motorola projections cited in various papers suggest that the number of electrons used to store a single bit in DRAM will decline down to a single electron at some time around 2010, thereby limiting further density improvements in conventional CMOS DRAM technology. The bounds for microprocessors are less clear, especially with emerging technologies such as Quantum Dot Transistors (QDT), with sizes of the order of 10 nm, as compared to current MOS technology devices which are at least twenty times larger (Good introductions to QDT technology are posted at www.ibm.com and the Department of Electrical Engineering, University of Minnesota.). While the first functioning QDT in 1997 resulted in much fanfare and hype, the reality is that even QDTs have geometry limits and thus density limits - the QDT at best postpones the inevitable crunch. It follows that extant and nascent semiconductor component technologies should be capable of supporting further density growth until at least 2010.

We cannot accurately predict further process improvements beyond that time, which accords well with Meads Rule' and its projection of 11 years for scientifically based projections. Is 2010 the ultimate, final, hard limit to performance growth ? The answer is no, since there remains considerable potential for performance growth in machine architectures. To date almost all architectural evolution seen in microprocessors has been little more than the reimplementation of architectural ideas used in 1960s and 1970s mainframes, minicomputers and supercomputers, made possible by larger transistor counts. We have seen little architectural innovation in recent decades, and only modest advances in parallel processing techniques.

The achievable performance growth resulting from the adoption of VLIW architectures remains to be seen. While these offer much potential for performance growth through instruction level parallelism, they do not address the problems of parallel computation on multiple processors, and it is unclear at this time how well they will scale up with larger numbers of execution units in processors. Much will depend on compiler technology. It would be naive to assume that we have already wholly exhausted the potential for architectural improvements in conventional Von-Neumann model stored program machines.

Indeed if history teaches us anything, it is that well entrenched technologies can be wiped out very rapidly by new arrivals: the demise of the core memory under the onslaught of the MOS semiconductor memory is a classical case study, as is the GMR read head on the humble disk drive, which rendered older head technologies completely uncompetitive over a two year period. A decade ago the notion of a 30 GB 3.5" hard disk for $500 would have been considered well and truly science fiction. It may well be that quantum physical barriers will not be the limiting factor in microprocessor densities and clock speeds, rather the problems of implementing digital logic to run at essentially microwave carrier frequencies will become the primary obstacle to higher clock speeds.

The problem is twofold. On chip, as the clock speed goes beyond a GigaHertz, the classical timing problems such as clock skew come into play, but also the parasitic inductances of wiring on chip will introduce resonances which in turn can result in problems such as timing jitter. Indeed, the whole timing problem becomes increasingly difficult. The other side of this problem is getting data in and out of the chip itself. Every pin has a stray capacitance and inductance associated with it, every track on the printed circuit board becomes a transmission line. A 250 picosecond pulse or strobe in such an environment is shorter in length than the tracks in the motherboard.

As a result, everything must be treated as a microwave RF distributed circuit, a delight for ECL generation dinosaurs, but agony for the TTL/CMOS generation of board designers. The current trend to integrate increasingly larger portions of the computer system on a single die will continue, alleviating the problem in the medium term, however a 2020 microprocessor running at a 60 GHz clock speed is an unlikely proposition using current design techniques. Vector processing supercomputers built from discrete logic components reached insurmountable barriers of this ilk at hundreds of MegaHertz, and have become a legacy technology as a result.

Do other alternatives to the monolithic Silicon chip exist ? Emerging technologies such as quantum computing (see the concurrent feature by Dr Bruce Mills) and nano-technology both have the potential to further extend performance beyond the obstacles currently looming on the 2010-2020 horizon. Quantum computing is at this stage at the conceptual level, and it remains to be seen whether practical computers can be built using these techniques. Nanotechnology has become the darling of sci-fi writers, although I must confess that I find the notion of a Babbage mechanical computer crafted from individual molecules just a little difficulty to imagine ! Again, it is a technology which is in its infancy and the timelines for practical systems remain very unclear.

Other alternatives also exist. Neural computing techniques, Prof Carver Mead argues, have the potential to deliver exponential performance growth with size, rather than speed, in the manner predicted for as yet unrealised highly parallel architectures. In simpler terms, both of these technologies aim to increase computer performance by making the performance scale with the size/complexity of the computer, rather than the clock speed. The intent in a sense is not unlike biological wetware processing, where intelligence typically scales with the volume of the cranial cavity. Highly parallel architectures, like neural computing, ideally exhibit the same property. In practice, performance growth tends to the logarithmic, with extant architectures. The holy grail of parallel processing, linear speedup, is at best achieved for small numbers of CPUs and slows down dramatically with complexity. The various hypercube class topologies have not proven to be the panacea many had hoped for.

Yet again, the computer architecture is not yet up to our longer term ambitions. It does however follow that while reaching the speed and density limits of semiconductor technology may mean the end of exponential growth in single chip density and clock speeds, but it is no guarantee that the exponential growth in compute performance will slow down. What we can predict with a high level of confidence is that Moore's Law will hold for the coming decade, and exponential growth is very likely to continue beyond that point. Greed can be a great motivator !

What Should We Expect ? Making short to medium term predictions is much less fraught with danger in comparison with gazing into the crystal ball and attempting to guess two decades ahead. Given that the quantum limit is somewhere around a decade away, we can reasonably safely use Moore's law to project densities and clock speeds for the next few years. The transistor count for a commodity 1 GHz CPU is around 30 million per die today.

Therefore by 2005-2010 dies with around 1 billion transistors should not be uncommon. What does a die with a billion transistors mean ? Current microprocessors require about 20-25 transistors per byte of on chip cache, overheads included. Lets assume half the die is used for cache - this means 20-25 Megabytes of high speed on chip cache is feasible. Enough to fit the ugliest database application into the cache. What other possibilities exist ? Let's consider a Cray-like vector processor.

The register storage for vector operands, assuming 64 bit doubles throughout, and four chained vector registers, would allow vector register depths into the thousands, making the Cray 1 look genuinely like a toy. Even assuming a 10 Megabyte on die L1/L2 cache arrangement. Let's assume a VLIW architecture. The translation cache for emulation of legacy CISC/RISC architectures could be Megabytes or more in size, still leaving ample transistors for dozens of execution units.

Transistors to burn ? We could pack almost all of the bus interface controllers on to a single die. This means the motherboard becomes little more than an elaborate backplane to support the various plug in I/O adaptors required, and the central bus controller.

What happens with DRAM ? Disregarding speed and committing wholly to density, a module with nine 8 Gigabit dies gives us easily 8 Gigabytes per module, which means a fully loaded desktop system has tens of Gigabytes of DRAM. Getting the required bandwidth between the CPU and the main memory will remain a tricky issue.

We could see the main memory embedded into the same ceramic chip carrier as the CPU, a highly likely approach since microprocessor optimised processes are usually quite different from DRAM processes, despite the nominally identical Silicon substrate material. This is however a little inflexible, and may not be entirely popular with the customer base. Commodity machines have tended to follow trends in Unix workstation motherboards, and this would suggest in the near term the likely use of a very large crossbar switch between multiple CPU and DRAM modules, the latter all socketed or slotted into the motherboard. Most of the motherboard would be passive wiring, crafted for the high clock speeds required.

Smart synchronous system busses with 256, 512 or more bits of width are very likely, with clock cycles of several hundred Megahertz. All is technically feasible once we can pack hundreds of millions of transistors into dies which clock at a GigaHertz or more. What do these trends suggest for a commodity machine in the 2005-2010 timescale ? Clock speeds of GigaHertz are almost certain, many Megabytes of full speed cache on die, Gigabytes of DRAM, hundreds of Gigabytes of disk storage. These are coarse metrics alone.

Architecturally the CPU in such a machine is likely to a highly parallel 64-bit VLIW engine, with a multi Megabyte translation cache allowing it to emulate dynamically any standard architecture for which it has translation mappings. Indeed, it might be capable of emulating any number of legacy architectures. It is not infeasible to expect the capability, with some decent concurrent effort in operating systems, to run binaries for different architectures under the one operating system, with no significant loss in performance.

Who then cares whether the application was originally compiled for an i86, Alpha, SPARC, PA, Power or other RISC/CIS architecture ? Where the operating systems are close enough in technology, such as Unix, this becomes quite feasible. Where they are further apart, the challenge is primarily in software. Whether we see genuine vector processing pipelines and register banks will depend largely upon market pressures.

Short vector units or SIMD processors are likely to be increasingly popular with the ongoing strong demand for multimedia. Long vector units may have to wait for the needs of increased instruction, data and translation caches to be satisfied, noting that a Cray 1 style engine uses only about 2048 bytes of vector register storage. These projections forward are all wholly based upon existing architecture and established design techniques, and therefore are highly probable outcomes.

What a commodity machine in 2010 will actually look like will be strongly dependent upon the market pressures in the intervening period, which will shape the evolutionary path of microprocessors. The question which remains unanswerable at this time is whether we can expect to see any radical breakthroughs in architecture, or fundamental technology, during this period. With quantum physical limits to the transistor looming on the horizon, the long term future of the industry will ride on them.

Note: portions of this article are derived from a paper presented by the author at the AOC 3rd EW Conference in Zurich, this May.

Artwork, graphic design, layout and text © 2004 - 2014 Carlo Kopp; Text © 2004 - 2014 Peter Goon; All rights reserved. Recommended browsers. Contact webmaster. Site navigation hints. Current hot topics.

Site Update Status: $Revision: 1.753 $ Site History: Notices and Updates / NLA Pandora Archive

Follow @APA_Updates